From the drawers of "I didn't realise how complicated that was" I was wondering the other day how to draw a line using just pixels. This turned out to be more complicated than I thought.
Normally in PHP you would use the imageline() function to draw a line between two points. The following block of code creates and image and draws a white line from the coordinates 50x,50y to 200x,150y.
// Generate image resource with a width an height of 250 pixels.
$im = imagecreatetruecolor(250, 250);
// Create a colour.
$white = imagecolorallocate($im, 255, 255, 255);
// Draw a white line from 50x,50y to 200x,150y.
imageline($im, 50, 50, 200, 150, $white);
// Write the image resource to a file called line.png.
imagepng($im, 'line.png');
// Destroy the image resource.
imagedestroy($im);
This creates an image that looks like this.

As an exercise I was looking at how to draw the same line by just drawing the pixels along the line. The starting point to this is with the function imagesetpixel(), which allows us to set a different colour to any pixel within the image. I knew that I had to step along the line and colour each pixel in the line bit by bit. After a bit of research I found Bresenham's line algorithm, which allows a line to be drawn between two points. Bresenham's line algorithm is one of a family of algorithms that allow lines to be drawn between one point and another, but I'm only going to concentrate on this algorithm in this post.
Bresenham's algorithm works by looking at raster points between the start and end points. A raster point is a point at which a pixel is displayed onto the screen and because the actual line between two points will go through a number of different pixels we need to decide which pixels best describe the line. The algorithm goes along the line and decides if pixels should be 'on' or 'off', thus drawing the line.
Actually, this isn't technically true. Let's take a line going from 0x,1y to 5x,4y. What we do is run along the x values from 0 to 5 and then decide if drawing a pixel at a certain point on the y axis by looking at the gradient of the line. If the endpoint is higher then draw the pixel higher and if the endpoint is lower, draw the pixel lower. The algorithm following the following equation (taken from Wikipedia).
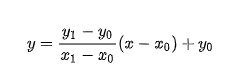
Before looping through the x coordinates we need to work out some values first.
$dx = $x1 - $x0;
$dy = $y1 - $y0;
$slope = $dy / $dx;
$pitch = $y0 - $slope * $x0;
This gives us the values of 0.6 for the slope and 1 for the pitch. For each step along the x coordinate we can then work out the position of the y coordinate by using the simplified equation.
$y = $slope * $x + $pitch;
Each point results in the following calculations.
| x | Calculation to work out y | y |
|---|
| 0 | 0.6 * 0 + 1 | 1 |
| 1 | 0.6 * 1 + 1 | 2 |
| 2 | 0.6 * 2 + 1 | 2 |
| 3 | 0.6 * 3 + 1 | 3 |
| 4 | 0.6 * 4 + 1 | 3 |
| 5 | n/a | 4 |
This produces pixels in the following places (the final pixel being just drawn in at the end).
.0123456
0.......
1x......
2.xx....
3...xx..
4.....x.
5.......
You might think that this is everything we need to do, but there is a problem when we try to calculate an upwards slope. The above calculations rely on the fact that the x value increases, so we need to add some code to take into account a line that starts at a high x value and decreases. We will also hit a problem if the end point is higher than the start point. We therefore need to either increment or decrement x or y in order to draw the line correctly.
I have seen examples on the internet where Bresenham's line algorithm is split into two parts where up and downward sloping lines are handled in different functions. This can be useful when highly optimising things, but generally a single function is fine.
Finally, we also need to add a tiny bit of code in case the start and end coordinates are the same as we don't need to run through any of this code.
The final code for the line drawing using Bresenham's line algorithm is as follows.
/**
* Draw a line using Bresenham's line algorithm.
*
* @param resource $im
* The image resource.
* @param int $x0
* The x part of the starting coordinate.
* @param int $y0
* The y part of the starting coordinate.
* @param int $x1
* The x part of the ending coordinate.
* @param int $y1
* The y part of the ending coordinate.
* @param int $colour
* The colour of the line, created from imagecolorallocate().
*/
function drawLine($im, $x0, $y0, $x1, $y1, $colour) {
if ($x0 == $x1 && $y0 == $y1) {
// Start and finish are the same.
imagesetpixel($im, $x0, $y0, $colour);
return;
}
$dx = $x1 - $x0;
if ($dx < 0) {
// x1 is lower than x0.
$sx = -1;
} else {
// x1 is higher than x0.
$sx = 1;
}
$dy = $y1 - $y0;
if ($dy < 0) {
// y1 is lower than y0.
$sy = -1;
} else {
// y1 is higher than y0.
$sy = 1;
}
if (abs($dy) < abs($dx)) {
// Slope is going downwards.
$slope = $dy / $dx;
$pitch = $y0 - $slope * $x0;
while ($x0 != $x1) {
imagesetpixel($im, $x0, round($slope * $x0 + $pitch), $colour);
$x0 += $sx;
}
} else {
// Slope is going upwards.
$slope = $dx / $dy;
$pitch = $x0 - $slope * $y0;
while ($y0 != $y1) {
imagesetpixel($im, round($slope * $y0 + $pitch), $y0, $colour);
$y0 += $sy;
}
}
// Finish by adding the final pixel.
imagesetpixel($im, $x1, $y1, $colour);
}
Running a few examples of this function with random coordinates produces the following image.

Bresenham's line algorithm is used quite extensively in lots of different applications but it isn't that great at creating anti-aliased lines so it doesn't get used when anti-aliasing is needed.
Incidentally, the imageline() function in PHP calls the gdImageLine() function from the GD library. As can be see from the source code of gdImageLine() this function actually implements the Bresenham's line algorithm. This is more complex (and much better tested!) than my simple example here, but it still follows the same basic rules.


Comments
curious .. have you been able to add 2 individual lines of text to an existing image?
Submitted by Kevin Brosnahan on Thu, 10/17/2019 - 14:05
PermalinkYou mean using something like imagettftext()?
Submitted by philipnorton42 on Thu, 10/17/2019 - 16:50
PermalinkAdd new comment